Sıralama Algoritmaları
Selam gençler ve bilgisayar başındayken genç hissedebilenler. Bilgisayar ile ilgili uzun zamandır bir şeyler yazıp çizmemiştim. Ara sıra babam evde tatil yaparken başında durmak durumunda olduğum manavdan yazıyorum bu yazıyı.
Burada internet olmadığı için yazıyı Word’de yazıyorum ve önceki geceden yazıyı yazabilmek için yapmam gereken araştırmaları yapıp, bulduğum bütün web sayfalarını bilgisayarda bir klasöre kaydettim. Şimdi eğlenceli bir iş günü beni bekliyor.
Sıralama algoritmaları bilgisayarcıların üzerinde çok düşünüp sürekli yeni icatlar çıkardıkları bir konu. O kadar çok sıralama algoritması icat etmişler ki, hepsini araştırıp bir yazıda yazsaydım hem benim için ölümcül bir eylem olacaktı, hem de okuyucu için korkutucu bir metin kitlesi ortaya çıkacaktı. O yüzden bu yazıda şu 6 sıralama algoritmasına değinmek istiyorum:
- Seçmeli Sıralama (Selection Sort)
- Eklemeli Sıralama (Insertion Sort)
- Kabuk Sıralaması (Shell Sort)
- Birleştirmeli Sıralama (Merge Sort)
- Hızlı Sıralama (Quick Sort)
- Kabarcık Sıralaması (Bubble Sort)
Kime göre neye göre seçtim veya sıraladım bunları? Ben de tam bilmiyorum. Araştırdım, kodlarını yazdım, hoşuma gidenleri yazdım, kodların uzunluğuna göre küçükten büyüğe sıraladım, listeye sonradan eklediklerim oldu, sırası bozuldu falan filan. Şimdi algoritmalarımızda biraz daha derine inelim.
1. Seçmeli Sıralama (Selection Sort)
1.1. Çalışma Mantığı
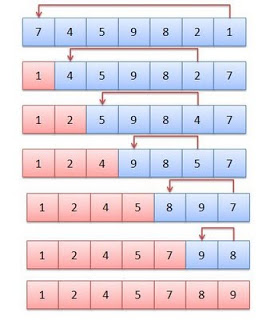
Bu algoritma bana göre düşünmesi en kolay sıralama algoritması. İlk elemandan son elemana kadar her elemanı kendinden sonra gelen kendinden küçük elemanların en küçüğü ile yer değiştiriyoruz. Örneğin aşağıdaki diziyi 3. elemanına kadar sıraladığımızı düşünelim ve daha sonra ne yapacağımıza bakalım.
{1, 2, 3, 10, 6, 4, 7}
Gördüğümüz gibi, 3. elemana kadar sıralanmış bir dizimiz var. Bu durumda şu anda 4. eleman olan 10’a bakmaktayız ve kuralımıza göre, 10’dan sonra gelen ve 10’dan küçük olan en küçük elemanı bulup 10 ile yerini değiştirmemiz gerekiyor. Bu adımda bu kurala uyan sayımız 4. Yerlerini değiştirdiğimizde dizimiz şu hale geliyor:
{1, 2, 3, 4, 6, 10, 7}
Üçüncü elemana baktığımıza göre bir sonraki adımda da dördüncü elemana bakıyoruz ve kuralı uyguluyoruz. Dizinin sonuna kadar böyle devam ettiğimizde tüm diziyi sıralamış oluyoruz.
1.2. Zaman ve Bellek Kullanımı
Kalburüstü sıralama algoritmaları genellikle en kötü durumda O(n2) zaman alırlar ve bu algoritma en iyi durumda bile O(n2) zaman aldığı için zaman açısından verimsiz bir algoritma olarak sınıflandırılıyor. En önemli avantajı bellek kullanımında O(1) ekstra alan kullanması. Bu avantajıyla da zaman açısından gerisinde kaldığı birçok gelişmiş algoritmayı geride bırakıyor. Birkaç elemandan oluşan dizileri sıralarken hızlı kod yazmak açısından bu algoritmayı kullanabilirsiniz.
1.3. Örnek Java Kodu
public static void selectionSort(int arr[]) {
for (int i = 0; i < arr.length; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
2. Eklemeli Sıralama (Insertion Sort)
2.1. Çalışma Mantığı
Bu algoritma dizinin 2. elemanından başlar ve son elemana varana kadar üzerine geldiği her elemanı,
o elemandan önce gelip de o elemandan büyük olan elemanlarla yer değiştirir.
Bu durumda işlem sırasında üzerine geldiğimiz bir elemanın solunda kalan elemanlar sıralı,
sağındakiler ise karışık düzende olacaktır.
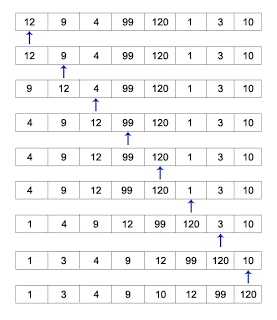
Örneğin a = {2,4,5,3,1,6} şeklinde bir dizimiz olsun
ve üzerine geldiğimiz eleman da a[3] = 3 olsun.
Görüldüğü gibi, üzerine geldiğimiz elemanın sol tarafı sıralı
ve sağ tarafı karışık düzende.
Bu durumda algoritma 3’ün solunda olup da 3’ten büyük olan elemanları birer eleman sağa kaydıracak
ve açılan boşluğa da 3’ü yerleştirecek.
Adım adım gidecek olursak:
{2,4,5,3,1,6} -> {2,4,5,5,1,6} -> {2,4,4,5,1,6} -> {2,3,4,5,1,6}.
Daha sonra bir sonraki elemana geçilerek a[4] = 1 elemanına gelinir
ve o da sola kaydırılarak {1,2,3,4,5,6} şeklindeki sıralı dizimizi buluruz.
Son eleman zaten dizideki en büyük eleman olduğu için herhangi bir yer değiştirme işlemi yapılmadı.
2.2. Zaman ve Bellek Kullanımı
Bu algoritma en iyi durumda O(n) ve en kötü durumda O(n2), yani ortalama olarak O(n2) zaman alıyor. Fazla karışık olmayan, yani neredeyse sıralı diyebileceğimiz diziler üzerinde çalıştırıldığında seçmeli sıralamaya göre zamanı çok daha verimli kullanıyor. Ek olarak O(1) bellek alanı kullanması açısından da birçok gelişmiş sıralama algoritmasını geride bırakıyor. Çok karmaşık ve büyük dizilerde, özellikle de küçük terimleri sonlarında olan dizilerde tavsiye etmiyorum.
2.3. Örnek Java Kodu
public static void insertionSort(int arr[]) {
for(int i = 1; i < arr.length; i++) {
int value = arr[i];
int j = i - 1;
while(j >= 0 && arr[j] > value) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = value;
}
}
3. Kabuk Sıralaması (Shell Sort)
Algoritmanın isminin(Shell Sort) kabuk sıralaması diye Türkçeye çevrilmesi komik olmuş çünkü algoritmanın ismi algoritmayı bulan kişinin(Donald Shell) de soyadı ve dolayısıyla algoritmanın kabuk ile hiçbir ilgisi yok. Neyse konumuz bu değil.
3.1. Çalışma Mantığı
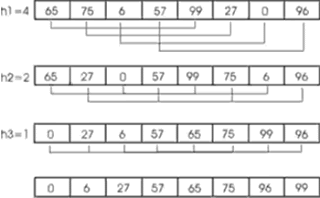
Yukarıda anlattığım eklemeli sıralama algoritmasını bir düşünelim. Çok büyük bir dizi üzerinde bu algoritmayı kullandığımızda, eğer dizinin küçük elemanları dizinin sonlarında duruyorsa, onları dizinin başına kaydırmak bizim için bir hayli zor bir işlem olacaktır. Şunu da biliyoruz ki eklemeli sıralama algoritması sıralıya yakın şekilde düzenlenmiş dizilerde çok daha hızlı çalışmakta. Bu durumda eklemeli sıralama algoritmasının biraz daha geliştirilmiş versiyonu olan kabuk sıralaması imdadımıza yetişiyor. Kabuk sıralaması, diziyi büyük parçalara bölüp bu parçaları bir tablonun satırlarıymış gibi alt alta düşünerek, bu tablonun sütunlarını eklemeli sıralama algoritmasıyla sıralı hale getiriyor. Daha sonra diziyi biraz daha küçük parçalara bölüp tekrar tekrar aynı işlemleri yapıyor ve en sonunda dizi elemanlarını birer birer ayırmış oluyor, yani tek sütun haline getirmiş oluyor ve o sütunu da eklemeli sıralama mantığıyla sıraladığında sıralama işlemi tamamlanmış oluyor. Bunu bu şekilde anlatmak çok zor olduğu için şimdi örnek bir dizi üzerinde düşünelim. Dizimiz şu şekilde olsun:
{13, 14, 94, 33, 82, 25, 59, 94, 65, 23, 45, 27, 73, 25, 39}
Bu diziyi ilk olarak 5’e böldüğümüzü varsayalım. Aşağıdaki tabloyu elde ediyoruz:
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
Şimdi bu tablonun sütunlarını sıralıyoruz ve şu tabloyu elde ediyoruz:
13 14 73 25 23
25 27 94 33 39
45 29 94 65 82
Bu durumda dizimizin yeni hali şu oluyor:
{14, 73, 25, 23, 13, 27, 94, 33, 39, 25, 59, 94, 65, 82, 45}
Şimdi bu diziyi 3’e böldüğümüzü düşünelim. Aşağıdaki tabloyu elde ediyoruz.
14 73 25
23 13 27
94 33 39
25 59 94
65 82 45
Şimdi bu tablonun sütunlarını sıralıyoruz ve aşağıdaki tablo ile diziyi elde ediyoruz.
14 13 25
23 33 27
25 59 39
65 73 45
94 82 94
{14, 13, 25, 23, 33, 27, 25, 59, 39, 65, 73, 45, 94, 82, 94}
Son olarak da dizimizi 1’e böldüğümüzü düşünürsek, basit bir eklemeli sıralama işlemi yaptığımızı ve elemanların neredeyse sıralanmış olduğunu görüyoruz. Basit birkaç işlem ile karmaşık bir diziyi eklemeli sıralama ile kolayca sıralayabileceğimiz bir dizi haline getirdik.
3.2. Zaman ve Bellek Kullanımı
Kabuk algoritması zaman olarak diziyi böldüğümüz parça sayısına göre değişmekte fakat en uygun atlama aralığı seçildiği zamanlarda en kötü durumda O(nlog2n) zamanda işini görüyormuş. Aşağıda vereceğim örnek kod ise işini O(n2) zamanda görmekte. Yaptığım testlerde sıralanmamış rastgele elemanlardan oluşan bir dizi üzerinde kabuk metodu eklemeli sıralama metodunun yaklaşık 200 katı daha hızlı çalıştı. Test sonuçlarını da yazının sonunda aktaracağım. Bellek kullanımına geldiğimizde ise algoritma sadece O(1) ekstra alana ihtiyaç duyuyor. Bellek kullanımı olarak yazdığım ilk iki algoritmadan farklı değil fakat zaman olarak ilk iki algoritmadan da daha iyi. Kodlama kolaylığını, bellek kullanımını ve hızını birlikte düşünürsek, ben kendime bu yazıdaki 6 algoritma içerisinden bu algoritmayı tavsiye ederim.
3.3. Örnek Java Kodu
public static void shellSort(int[] a) {
for (int increment = a.length / 2; increment > 0; increment = (increment == 2 ? 1 : (int) Math.round(increment / 2.2))) {
for (int i = increment; i < a.length; i++) {
int temp = a[i];
for (int j = i; j >= increment && a[j - increment] > temp; j -= increment){
a[j] = a[j - increment];
a[j - increment] = temp;
}
}
}
}
4. Birleştirmeli Sıralama (Merge Sort)
4.1. Çalışma Mantığı
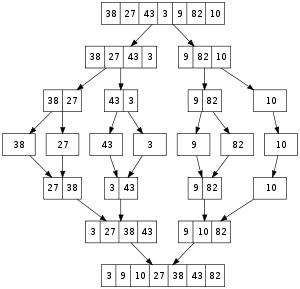
Sıralı iki diziyi yine sıralı olacak şekilde birleştirmek kolay bir işlemdir. Dizilerin ilk elemanlarını karşılaştırırsınız ve küçük olanını alırsınız. Daha sonra diğer dizide kalan almadığınız elemanı diğer dizinin ikinci elemanıyla karşılaştırırsınız ve yine küçük olanı alırsınız. İki dizide de eleman kalmayıncaya kadar bu böyle sürüp gider. Birleştirmeli sıralama algoritmamız da buna benzer bir mantık kullanıyor. Diziyi ikiye bölüp oluşan alt kümeleri tekrar birleştirmeli sıralama algoritmasına alıyor ve böylece dizi sürekli ikiye bölünmüş oluyor. Elemanları ikişerli olarak karşılaştırıp sıralı biçimde birleştiriyor, daha sonra bu iki elemanlı alt kümeleri sıralı biçimde birleştirerek dört elemanlı alt kümeler elde ediyor. Böyle devam ettiğimizde, örneğin dizimiz 16 elemanlı ise elimizde 8 elemanlı, elemanları sıralı iki alt küme kalıyor. Bu alt kümeleri de aynı şekilde sıralı biçimde birleştirdiğimiz zaman dizimiz sıralanmış oluyor. Aşağıdaki resimde bu işlemleri daha net görebiliyoruz.
4.2. Zaman ve Bellek Kullanımı
Bu algoritma araştırdığım kaynaklara göre ortalama ve en kötü durumda hayatımızdan O(nlogn) zaman götürüyor. Teorik olarak yukarıdaki 3 algoritmadan da kısa zamanda işini görüyor denilebilir fakat yaptığım birkaç testte Shell metodunun birleştirme metodunun önüne geçtiğini gözlemledim. Bellek kullanımında ise bu metodun önceki yöntemlere göre dezavantajı var. Birleştirmeli sıralama O(n)’lik bir ekstra bellek kullanıyor ki bu da boyutu büyük elemanlara sahip çok elemanlı dizileri sıralarken kendini fazlasıyla belli edecektir. Hem bellek kullanımının hem de performansın önemli olduğu durumlarda ben Shell metodunu tavsiye ediyorum.
4.3. Örnek Java Kodu
public static int[] mergeSort(int arr[]) {
if( arr.length <= 1 ) {
return arr;
} else {
int middle = (int)(arr.length/2);
int left[] = new int[middle];
int right[] = new int[arr.length-middle];
for( int i=0; i<middle; i++) {
left[i] = arr[i];
}
for( int i=middle; i<arr.length; i++ ) {
right[i-middle] = arr[i];
}
left = mergeSort(left);
right = mergeSort(right);
int result[] = merge(left, right);
return result;
}
}
public static int[] merge(int left[], int right[]) {
int result[] = new int[left.length + right.length];
int i=0, posLeft = 0, posRight = 0;
while(left.length > posLeft && right.length > posRight ) {
if( left[posLeft] <= right[posRight] ) {
result[i] = left[posLeft];
posLeft++;
} else {
result[i] = right[posRight];
posRight++;
}
i++;
}
if( left.length > posLeft ) {
for(; posLeft<left.length; posLeft++) {
result[i] = left[posLeft];
i++;
}
}
if( right.length > posRight ) {
for(; posRight<right.length; posRight++) {
result[i] = right[posRight];
i++;
}
}
return result;
}
5. Hızlı Sıralama (Quick Sort)
5.1. Çalışma Mantığı
Hızlı sıralama algoritması, verilen dizinin ortasına yakın bir yerinden bir pivot eleman seçer ve pivottan büyük elemanları sağa, pivottan küçük elemanları sola kaydırır. Bu işlemi yaptıktan sonra pivot elemanın solundaki ve sağındaki dizilerden ayrı ayrı pivot elemanlar seçer ve o dizileri kendi içerisinde tekrar bu işleme tabi tutar. Rekürsif bir şekilde bu işlem devam ettikten sonra tüm dizi sıralanmış olur.
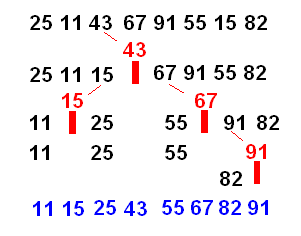
5.2. Zaman ve Bellek Kullanımı
Bu algoritma en kötü durumda O(n2), ortalamada ise O(nlogn) zaman alır. Bu sayede performans olarak yukarıdaki tüm metotların üzerine çıkar. Bellek kullanımı olarak ise en kötü durumda O(n) ekstra alan kullanır ki bu da rekürsif olmasından kaynaklanır.
5.3. Örnek Java Kodu
public static void quickSort(int arr[], int left, int right) {
if( left < right ) {
int pivotIndex = (int) (left + (right-left)/2);
int pivotNewIndex = partition(arr, left, right, pivotIndex);
quickSort(arr, left, pivotNewIndex - 1);
quickSort(arr, pivotNewIndex + 1, right);
}
}
public static int partition(int arr[], int left, int right, int pivotIndex) {
int pivotValue = arr[pivotIndex];
arr[pivotIndex] = arr[right];
arr[right] = pivotValue;
int storeIndex = left;
for(int i=left; i<right; i++) {
if( arr[i] < pivotValue ) {
int temp = arr[i];
arr[i] = arr[storeIndex];
arr[storeIndex] = temp;
storeIndex++;
}
}
int temp = arr[right];
arr[right] = arr[storeIndex];
arr[storeIndex] = temp;
return storeIndex;
}
6. Kabarcık Sıralaması (Bubble Sort)
Bunu anlatmayı düşünmüyordum fakat sonra popülaritesine aldanıp listemin sonuna ekleyiverdim. Eğlenceli fakat yorucu bir algoritma.
6.1. Çalışma Mantığı
Mantık ve kodlama olarak çok basit fakat nasıl çalışacağını düşündüğümüzde işlemcinin canını sıkabilecek kadar çok işlem yapan bir algoritma. Dizinin başından başlıyor ve sonuna kadar tüm elemanları kendisinden önceki eleman ile karşılaştırıp, gerekirse yerlerini değiştiriyor. Bu şekilde diziyi dizi tamamen sıralanana kadar tekrar tekrar baştan sona tarıyor. Dizinin tamamen sıralandığını, yani yer değiştirecek hiçbir eleman kalmadığını anladığında çalışmayı durduruyor ve sıralama bitmiş oluyor.
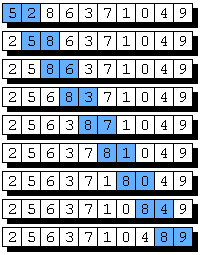
6.2. Zaman ve Bellek Kullanımı
En kötü durum testinde bu sayfada yazdığım bütün algoritmalardan daha fazla zaman aldığını göreceksiniz zaten. Algoritma en kötü durumda O(n2) zaman alıyor. Bellek kullanımında ise sadece O(1)’lik ek alana ihtiyaç duyuyor. Küçük ve neredeyse sıralı olan dizilerde uygulanabilir fakat büyük dizilerde kesinlikle tavsiye etmiyorum.
6.3. Örnek Java Kodu
public static void bubbleSort(int arr[]) {
boolean swapped = false;
do {
swapped = false;
for(int i=1; i<arr.length; i++) {
if( arr[i-1] > arr[i] ) {
int temp = arr[i];
arr[i] = arr[i-1];
arr[i-1] = temp;
swapped = true;
}
}
} while(swapped);
}
7. Algoritmalar Zamana Karşı
Aslında bu bölümde sadece aşağıdaki tabloyu çizip bırakacaktım fakat dizileri 500.000 eleman ile denediğim için 25 dakikaya kadar uzayan algoritmalarım oldu. Bu yüzden biraz da üzerinde konuşayım dedim. Dediğim gibi, dizilerde beş yüz bin eleman kullandım. Bu kadar uzun süreceğini biliyordum fakat jeton biraz geç düştü diyelim. Tabloda gördüğümüz gibi, Seçmeli Sıralama algoritması dizi sıralı olsa bile çok fazla zaman alıyor. Kabarcık Sıralamasını sıralamadan saymazsak en fazla zaman alan algoritma diyebiliriz. Eklemeli Sıralama ve Kabarcık Sıralaması algoritmaları sıralı diziler üzerinde müthiş bir zaman elde etmekte fakat işimiz sıralanmamış dizileri sıralamak olduğu için sıralı diziler üzerinde yaptıkları hızın bizim için istatistikten başka bir anlamı yok. Burada eğer bellek kullanımı sorun yaratabilecek bir diziden bahsetmiyorsak Hızlı Sıralama algoritmasını, eğer bellek kullanımı bizim için önemliyse Kabuk Sıralamasını tavsiye ediyoruz.
| Algoritma | Sıralı Dizi Üzerinde (ms) | Tersten Sıralı Dizi Üzerinde (ms) | Rastgele Sıralı Dizi Üzerinde (ms) |
|---|---|---|---|
| Seçmeli Sıralama (Selection Sort) |
583334 |
511961 |
516530 |
| Eklemeli Sıralama (Insertion Sort) |
10 |
407946 |
234287 |
| Kabuk Sıralaması (Shell Sort) |
80 |
100 |
230 |
| Birleştirmeli Sıralama (Merge Sort) |
260 |
230 |
330 |
| Hızlı Sıralama (Quick Sort) |
60 |
90 |
160 |
| Kabarcık Sıralaması (Bubble Sort) |
10 |
1536317 |
2062972 |
Kodlarımda, açıklamalarımda, dilbilgisi, imla veya noktalamada bir hatamı gördüyseniz yorum olarak geri bildirim bırakın bana. Umarım faydalı bir yazı olur.